¿Por qué no seguir la recomendación del IETS?

Por: Hoover Quitian-Reyes

Primera entrega: El uso incorrecto de la función de probabilidad dependiente del tiempo

Es importante aclarar que, en esta serie de publicaciones del blog, no se afirma que el Instituto de Evaluaciones de Tecnologías en Salud (IETS) haya realizado recomendaciones incorrectas en su manual de evaluaciones económicas. Si se revisa con atención la redacción del manual, este contiene recomendaciones que constituyen puntos de buena práctica y no interfiere con el diseño metodológico de las evaluaciones. Por el contrario, se enfatiza en que cada evaluación es distinta y requiere la justificación de cada uno de los elementos de la metodología.  

El problema surge de algunos autores que han optado por usar a su conveniencia algunos ejemplos, referencias y ayudas a las decisiones metodológicas incluidas en el manual, para no tener que detallar su metodología, o para evadir su responsabilidad de justificar su aplicabilidad en la evaluación económica que realizan y su contexto. Lo que hacen estos autores es justificar sus decisiones metodológicas tan solo indicando que se trata de una recomendación del IETS. Con ese artilugio, tales autores asaltan la buena fe tanto del IETS como de los lectores y evaluadores, porque buscan dejar a esa institución sin la capacidad de objetar, y a los lectores y evaluadores les trasmiten la idea errónea de que la evaluación se realizó adecuadamente.

Son varios los atajos que se toman con amparo en supuestas recomendaciones del IETS. Digo ‘supuestas’ porque en algunos casos no es cierto que el IETS haya realizado la recomendación. De esos ‘atajos’, que no han sido recomendados explícitamente por el IETS, pero que sí aparecen en algunos de los textos que se referencian en el manual, tal vez el que tiene las consecuencias más nocivas, para las estimaciones sobre efectividad de las evaluaciones económicas, es el uso indiscriminado de la función que describe la probabilidad de ocurrencia de un evento como ‘uno menos el número neperiano, elevado a una potencia compuesta por la multiplicación entre una constante negativa y el periodo que se está simulando’.

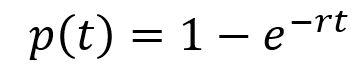
En dicha función, r es una tasa constante que debe calcularse y t representa al periodo. Es comúnmente empleada cuando se construyen modelos de Markov complejos porque se reconoce que la probabilidad depende del tiempo. Quienes no están familiarizados con la teoría de la probabilidad, pueden interpretar que esa función rige siempre la relación entre la probabilidad y el tiempo, que es una especie de ley natural de la probabilidad. Lo cierto es que NO existe una función que gobierne siempre la relación entre la probabilidad y el tiempo, es menester construir una función para cada caso particular.

La mencionada función tiene una característica que la hace candidata a ser utilizada como función de probabilidad: está acotada entre cero y uno, para todos los valores teóricos posibles de la variable que representa el periodo. Nada, absolutamente nada, garantiza que pueda describir adecuadamente la probabilidad de ocurrencia de algún evento de interés. Puede emplearse cualquier otra función que produzca valores consecuentes con la teoría de la probabilidad y, más importante aún, que describa el comportamiento esperado del fenómeno estudiado. Desde mi experiencia en el campo, el siguiente sería el procedimiento de cuatro pasos que sugiero:

1. Consultar con los expertos clínicos, y revisar en la literatura, cuál se espera que sea el comportamiento de la probabilidad con relación al tiempo. Esto es determinar si la relación es creciente o decreciente, si acelera o desacelera (concavidad o convexidad) y si existen periodos críticos o umbrales luego de los cuáles el comportamiento cambie considerablemente.
2. Construir una función, a manera de conjetura, que tenga la variable tiempo y cuya forma pueda describir lo que se estableció en el primer paso. Para comprobarlo, es necesario realizar el gráfico para los valores posibles de la variable tiempo. No se requiere que la función esté acotada entre cero y uno para cualquier valor de la variable tiempo. Debido a que en las evaluaciones económicas de tecnologías sanitarias se simulan cohortes, solo se debe estudiar el comportamiento de la función para los valores permitidos de la variable tiempo, es decir, aquellos que no signifiquen sobrepasar la esperanza de vida empleada.
3. Estimar los parámetros de la función propuesta en el segundo paso, de forma que sea capaz de producir los valores conocidos, es decir, las probabilidades encontradas en la literatura. Por ejemplo, si en literatura se reporta la probabilidad de ocurrencia del evento luego de cinco años de seguimiento, suponiendo que los ciclos sean anuales, la función propuesta debería replicar ese mismo valor cuando la variable de periodo adquiera valor de cinco.
4. Verificar que, con los parámetros estimados, además de replicar los valores de la literatura, la función produce un gráfico que describe el comportamiento establecido en el paso uno. De lo contrario, es necesario repetir los pasos, del dos al cuatro, hasta encontrar una función adecuada.

En este punto hay que preguntarse qué tanto puede afectar a las estimaciones el no emplear una función adecuada. No sería de importancia si se pudiera comprobar que, aunque el procedimiento de usar la mencionada función no es teóricamente adecuado, se consiguen estimaciones que no son muy distantes de lo que se obtendría siguiendo los cuatro pasos anteriormente sugeridos. Infortunadamente, no es posible tener una estimación del tamaño promedio, o la dirección, del sesgo que se genera, porque en cada evaluación el efecto será distinto. No obstante, basta con observar que la función que generalmente se usa supone que la relación entre la probabilidad y el tiempo es positiva (primera derivada positiva) y se desacelera (segunda derivada negativa), lo que significa que en todos los casos en los que eso no sea cierto, los modelos realizados generaron estimaciones que no incorporaron adecuadamente la naturaleza de los eventos.

En cuanto a porqué es tan común que en las evaluaciones económicas de tecnologías publicadas para Colombia, que acudieron a modelos de Markov, se haya empleado, en todas las transiciones, la mencionada fórmula, existen dos razones. Una es el desconocimiento. Autores con poca comprensión de la teoría de la probabilidad, que interpretan incorrectamente los textos en los que aparece. Algunos de ellos gozan de reconocimiento y han publicado numerosas evaluaciones, pero su formación académica está en torno a otras disciplinas y no han dedicado el tiempo suficiente a esos temas. Casos que, dicho sea de paso, existen porque seguimos creyendo que el título académico de una persona puede ser empleado como argumento. La segunda razón es querer tomar el atajo. Autores que aprovechan que la función está en varias publicaciones y emplean ese hecho como patente de corso.

Infortunadamente, entre más estudios se publican con ese tipo de fallas metodológicas, más se normalizan y se genera en la opinión, tanto en la especializada como en la que no, la idea de que tales fallas son procedimientos correctos. Las razones por las que esos estudios son publicados en revistas que se supone realizan una evaluación por pares académicos pueden ser tema para otra entrada de este blog. Hasta aquí esta primera entrada de la serie. En la siguiente entrega, hablaré de las recomendaciones explícitas de IETS, en materia de costos, que ya están desactualizadas.

Si este tema fue de su interés y tiene preguntas al respecto, necesita ayuda con algún problema de modelamiento, o quiere que hable de otro aspecto metodológico de las evaluaciones económicas de tecnologías en salud, por favor escríbame a hoover.quitian@hqr.com.co. Con gusto haré lo que pueda para ser de ayuda.